Giochi di parole - Un trucco speciale, dove solo la matematica può dare una spiegazione
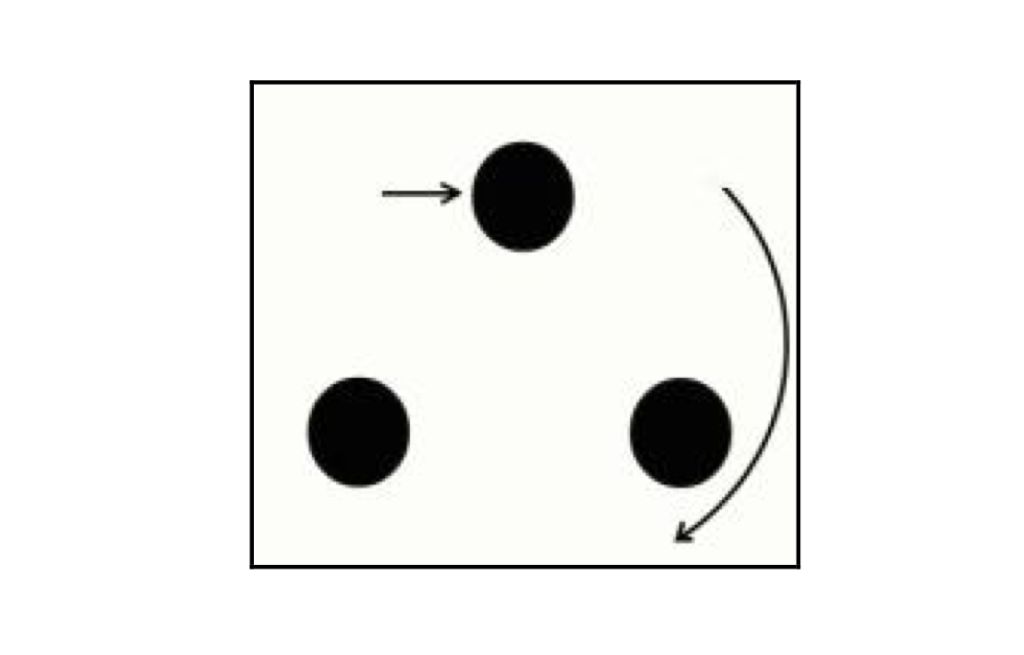
1. Capovolgete sul tavolo tre bicchierini non trasparenti, disponendoli ai vertici di un ipotetico triangolo equilatero.
2. Mostrate al pubblico la formula qui di seguito riportata, affermando che è stata ricavata da una misteriosa iscrizione trovata sul sarcofago del faraone Tutankhamon e che dona poteri paranormali a chi la usa in particolari condizioni:
P = X3Y–XY3,
3. Per verificare l’attendibilità della vostra affermazione, chiamate uno spettatore (di buona volontà…) e, dopo aver girato le spalle al pubblico, fornitegli le seguenti istruzioni:
a) attribuisci due valori interi positivi alle incognite X e Y, scegliendoli a tuo piacere, con il solo accorgimento che sia: X>Y;
b) ricava il valore che, così, viene ad assumere la P (ad esempio, se lo spettatore scegliesse X = 4 ed Y = 2, dovrebbe calcolare: P·= 43·2–4·23 = 64·2–4·8 = 128–32 = 96);
c) somma tra loro le cifre del risultato ottenuto, ripetendo questo procedimento finché non ti rimane una sola cifra (nel nostro esempio, otterrebbe: 9+6 = 15; 1+5 = 6);
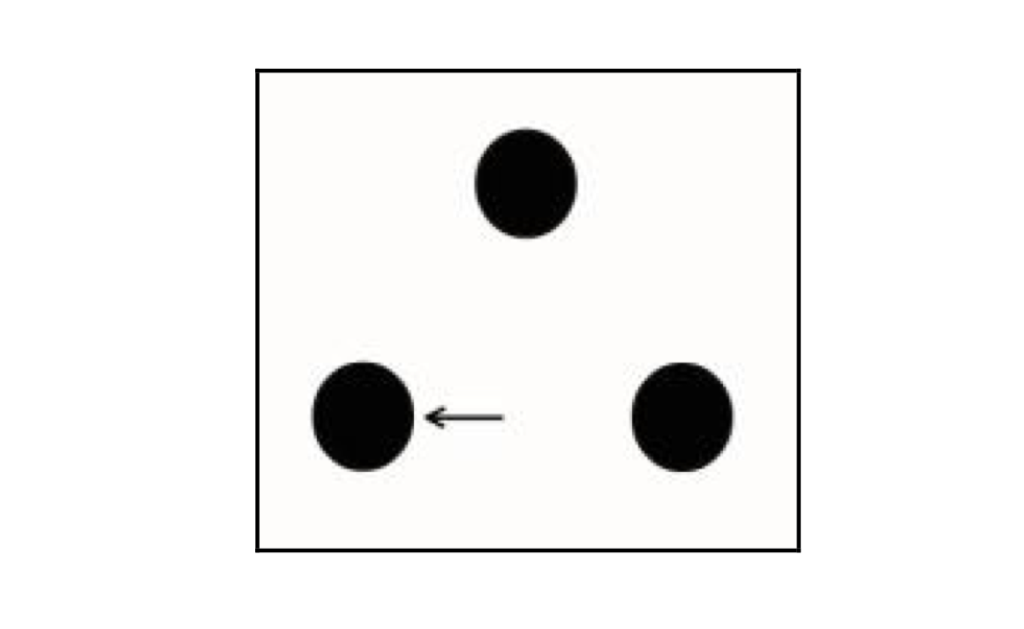
d) conta un bicchierino alla volta, in senso orario a partire da quello posto più in alto, un numero di volte pari al valore della cifra risultante;
e) poni una moneta sotto il bicchierino sul quale si è fermato il tuo conteggio.
6. Voltatevi verso il tavolo e, senza esitazione alcuna, sollevate il bicchierino sotto il quale si trova la moneta. A tale scopo, tenete presente che, al termine di tutte le operazioni sopra descritte, se non saranno stati commessi errori, il bicchierino sotto il quale si troverà la moneta sarà sempre quello posto in basso a sinistra.
Per dimostrare che non avete indovinato per caso, potete replicare questa stessa performance, con altri spettatori, una quantità di volte a vostra discrezione.
Spiegazione del trucco
In base a una curiosità matematica di antica data (risalente ai tempi di Tutankhamon?), scelti due numeri interi qualsiasi, o almeno uno dei due è un multiplo di 3, oppure lo è la loro somma o la loro differenza. Quindi, essendo sicuri che, tra i quattro numeri: X, Y, (X+Y) e (X–Y), uno almeno è multiplo di 3, deve essere un multiplo di 3 anche il loro prodotto: P = XY(X+Y)(X–Y). Considerando che: (X+Y)(X–Y) =, si può porre: P = XY(X+Y)(X–Y) = XY(X2–Y2); ovvero: P = X3Y–XY3.
Di conseguenza, indipendentemente dai valori di X e Y (purché X > Y), il numero P risultante dalla nostra formula sarà sempre un multiplo di 3. Siccome, per un noto criterio di divisibilità, la somma delle cifre di un multiplo di 3 è ancora un multiplo di 3, il risultato delle operazioni che abbiamo fatto svolgere allo spettatore potrà essere uguale solamente a: 3, 6 o 9. Per cui, il conteggio effettuato sui bicchierini, finirà inevitabilmente su quello in basso a sinistra (cioè il terzo in quest’ordine).